最短路径:从某顶点出发,沿图的边到达另一顶点所经过的路径中,各边上权值之和最小的一条路径。
1.单源点到其余各顶点的最短路径
给定带权有向图G和源点v,求从v到G中其余各顶点的最短路径。
迪杰斯特拉(Dijkstra)提出了一个按路径长度递增的次序产生最短路径的算法。
Dijkstra算法:
基本思想:这个算法的过程有比prim算法的过程稍微多一点点步骤,但是思想确实巧妙的,也是贪心原理,它的目的是求某个源点到目的点的最短距离,总的来说,dijkstra算法也就是求某个源点到目的点的最短路,求解的过程也就是求源点到整个图的最短距离,次短距离,第三短距离等等(这些距离都是源点到某个点的最短距离)。。。。。求出来的每个距离都对应着一个点,也就是到这个点的最短距离,求的也就是原点到所有点的最短距离,并且存在了一个二维数组中,最后给出目的点就能直接通过查表获得最短距离。
第1步:以源点(假设是s1)为开始点,求最短距离,如何求呢? 与这个源点相邻的点与源点的距离全部放在一个数组dist[]中,如果不可达,dist[]中为最大值,这里说一下,为什么要是一维数组,原因是默认的是从源点到这个一维数组下标的值,只需要目的点作为下标就可以,这时从源点到其他点的最短的“一”条路径有了,只要选出dist[]中最小的就行(得到最短路径的另一个端点假设是s2)。
第2步:这时要寻找源点(假设是s1)到另外点的次短距离,这个距离或者是dist[]里面的值,或者是从第1步中选择的那个最短距离 + 从找到点(假设是s2)出发到其他点的距离(其实这里也是一个更新操作,更新的是dist[]里面的值),如果最短距离 + 从这点(假设是s2)到其他点的距离,小于dist[]里面的值,就可以更新dist[]数组了,然后再从dist[]数组中选一个值最小的,也就是第“二”短路径(次短路径)。
第3步:寻找第“三”短路径,这时同上,第二短路径的端点(s3)更新与之相邻其他的点的dist[]数组里面的值。
第4步:重复上述过程n – 1次(n指的是节点个数),得出结果,其实把源点到所有点的最短路径求出来了,都填在了dist[]表中,要找源点到哪个点的最短路,就只需要查表了。

算法步骤:
① 令S={Vs} ,用带权的邻接矩阵表示有向图,对图中每个顶点Vi按以下原则置初值:

② 选择一个顶点Vj ,使得:dist[j]=Min{ dist[k]| Vk∈V-S },Vj就是求得的下一条最短路径终点,将Vj 并入到S中,即S=S∪{Vj} 。
③ 对V-S中的每个顶点Vk ,修改dist[k],方法是:
若dist[j]+Wjk<dist[k],则修改为:dist[k]=dist[j]+Wjk (“Vk∈V-S )
④ 重复②,③,直到S=V为止。
代码实现:
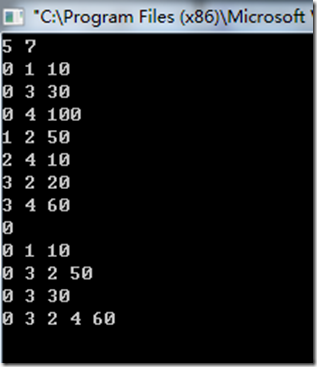
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 | #include <iostream> #include<stack> #define M 100 #define N 100 using namespace std; typedef struct node { int matrix[N][M]; //邻接矩阵 int n; //顶点数 int e; //边数 }MGraph; void DijkstraPath(MGraph g,int *dist,int *path,int v0) //v0表示源顶点 { int i,j,k; bool *visited=(bool *)malloc(sizeof(bool)*g.n); for(i=0;i<g.n;i++) //初始化 { if(g.matrix[v0][i]>0&&i!=v0) { dist[i]=g.matrix[v0][i]; path[i]=v0; //path记录最短路径上从v0到i的前一个顶点 } else { dist[i]=INT_MAX; //若i不与v0直接相邻,则权值置为无穷大 path[i]=-1; } visited[i]=false; path[v0]=v0; dist[v0]=0; } visited[v0]=true; for(i=1;i<g.n;i++) //循环扩展n-1次 { int min=INT_MAX; int u; for(j=0;j<g.n;j++) //寻找未被扩展的权值最小的顶点 { if(visited[j]==false&&dist[j]<min) { min=dist[j]; u=j; } } visited[u]=true; for(k=0;k<g.n;k++) //更新dist数组的值和路径的值 { if(visited[k]==false&&g.matrix[u][k]>0&&min+g.matrix[u][k]<dist[k]) { dist[k]=min+g.matrix[u][k]; path[k]=u; } } } } void showPath(int *path,int v,int v0) //打印最短路径上的各个顶点 { stack<int> s; int u=v; while(v!=v0) { s.push(v); v=path[v]; } s.push(v); while(!s.empty()) { cout<<s.top()<<" "; s.pop(); } } int main(int argc, char *argv[]) { int n,e; //表示输入的顶点数和边数 while(cin>>n>>e&&e!=0) { int i,j; int s,t,w; //表示存在一条边s->t,权值为w MGraph g; int v0; int *dist=(int *)malloc(sizeof(int)*n); int *path=(int *)malloc(sizeof(int)*n); for(i=0;i<N;i++) for(j=0;j<M;j++) g.matrix[i][j]=0; g.n=n; g.e=e; for(i=0;i<e;i++) { cin>>s>>t>>w; g.matrix[s][t]=w; } cin>>v0; //输入源顶点 DijkstraPath(g,dist,path,v0); for(i=0;i<n;i++) { if(i!=v0) { showPath(path,i,v0); cout<<dist[i]<<endl; } } } return 0; } |
运行结果:
2.每一对顶点之间的最短路劲
给定带权有向图G=(V, E),对任意顶点vi,vj∈V(i≠j),求顶点vi到顶点vj的最短路径。
解决办法1:每次以一个顶点为源点,调用Dijkstra算法n次。显然,时间复杂度为O(n3)。
解决办法2:弗洛伊德提出的求每一对顶点之间的最短路径算法——Floyd算法,其时间复杂度也是O(n3),但形式上要简单些。
Floyd算法:
Floyd算法的基本思想如下:从任意节点A到任意节点B的最短路径不外乎2种可能,1是直接从A到B,2是从A经过若干个节点到B,所以,我们假设dist(AB)为节点A到节点B的最短路径的距离,对于每一个节点K,我们检查dist(AK) + dist(KB) < dist(AB)是否成立,如果成立,证明从A到K再到B的路径比A直接到B的路径短,我们便设置 dist(AB) = dist(AK) + dist(KB),这样一来,当我们遍历完所有节点K,dist(AB)中记录的便是A到B的最短路径的距离。
很简单吧,代码看起来可能像下面这样:
1 2 3 4 5 6 7 8 9 | for (int i=0; i<n; ++i) { for (int j=0; j<n; ++j) { for (int k=0; k<n; ++k) { if (dist[i][k] + dist[k][j] < dist[i][j] ) { dist[i][j] = dist[i][k] + dist[k][j]; } } } } |
但是这里我们要注意循环的嵌套顺序,如果把检查所有节点K放在最内层,那么结果将是不正确的,为什么呢?因为这样便过早的把i到j的最短路径确定下来了,而当后面存在更短的路径时,已经不再会更新了。

图中红色的数字代表边的权重。如果我们在最内层检查所有节点K,那么对于A->B,我们只能发现一条路径,就是A->B,路径距离为9,而这显然是不正确的,真实的最短路径是A->D->C->B,路径距离为6。造成错误的原因就是我们把检查所有节点K放在最内层,造成过早的把A到B的最短路径确定下来了,当确定A->B的最短路径时dist(AC)尚未被计算。所以,我们需要改写循环顺序,如下:
1 2 3 4 5 6 7 8 9 | for(int k=1; k<=n; k++) { for(int i=1; i<=n; i++) { for(int j=1; j<=n; j++) { if(!(dist[i][k]==Inf||dist[k][j]==Inf)&&dist[i][j] > dist[i][k] + dist[k][j]) { dist[i][j] = dist[i][k] + dist[k][j]; } } } } |
Floyd算法另一种理解DP,为理论爱好者准备的,上面这个形式的算法其实是Floyd算法的精简版,而真正的Floyd算法是一种基于DP(Dynamic Programming)的最短路径算法。设图G中n 个顶点的编号为1到n。令c [i, j, k]表示从i 到j 的最短路径的长度,其中k 表示该路径中的最大顶点,也就是说c[i,j,k]这条最短路径所通过的中间顶点最大不超过k。因此,如果G中包含边<i, j>,则c[i, j, 0] =边<i, j> 的长度;若i= j ,则c[i,j,0]=0;如果G中不包含边<i, j>,则c (i, j, 0)= +∞。c[i, j, n] 则是从i 到j 的最短路径的长度。对于任意的k>0,通过分析可以得到:中间顶点不超过k 的i 到j 的最短路径有两种可能:该路径含或不含中间顶点k。若不含,则该路径长度应为c[i, j, k-1],否则长度为 c[i, k, k-1] +c [k, j, k-1]。c[i, j, k]可取两者中的最小值。状态转移方程:c[i, j, k]=min{c[i, j, k-1], c [i, k, k-1]+c [k, j, k-1]},k>0。这样,问题便具有了最优子结构性质,可以用动态规划方法来求解。
数组dist[n][n]:存放在迭代过程中求得的最短路径长度。迭代公式:

完整代码:
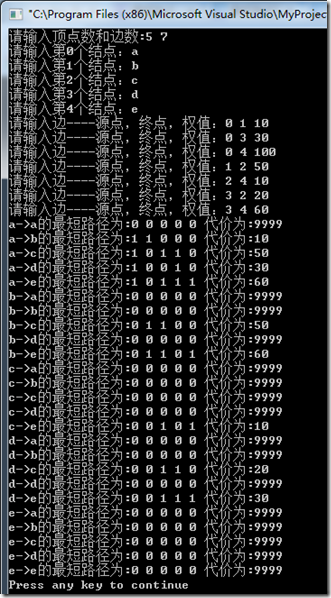
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 | #include "stdio.h" #include "stdlib.h" #define MAX 20 #define INFINITY 9999 typedef bool PathMatrix[MAX+1][MAX+1][MAX+1]; typedef int DistanceMatrix[MAX+1][MAX+1]; typedef struct { int vexnum,arcnum; char vexs[MAX+1]; int arcs[MAX+1][MAX+1]; }MGraph; void CreateDN(MGraph &G) { int i,j,k,v1,v2,w; printf("请输入顶点数和边数:"); scanf("%d %d",&G.vexnum,&G.arcnum); for(i=0;i<G.vexnum;i++) { getchar(); printf("请输入第%d个结点:",i); scanf("%c",&G.vexs[i]); } for(i=0;i<G.vexnum;i++) for(j=0;j<G.vexnum;j++) G.arcs[i][j]=INFINITY; for(k=0;k<G.arcnum;k++) { printf("请输入边----源点,终点,权值:"); scanf("%d %d %d",&v1,&v2,&w); G.arcs[v1][v2]=w; } } void ShortestPath_FLOYD(MGraph G,PathMatrix &P,DistanceMatrix &D) { int v,w,u,i; for(v=0;v<G.vexnum;++v) for(w=0;w<G.vexnum;++w) { D[v][w]=G.arcs[v][w]; for(u=0;u<G.vexnum;++u) P[v][w][u]=false; if (D[v][w]<INFINITY) { P[v][w][v]=true; P[v][w][w]=true; } } for(u=0;u<G.vexnum;++u) for(v=0;v<G.vexnum;++v) for(w=0;w<G.vexnum;++w) if (D[v][u]+D[u][w]<D[v][w]) { D[v][w]=D[v][u]+D[u][w]; for(i=0;i<G.vexnum;++i) P[v][w][i]=P[v][u][i]||P[u][w][i]; } } void main() { MGraph G; int i,j,k; CreateDN(G); PathMatrix p; DistanceMatrix D; ShortestPath_FLOYD(G,p,D); for(i=0;i<G.vexnum;i++) for(j=0;j<G.vexnum;j++) { printf("%c->%c的最短路径为:",G.vexs[i],G.vexs[j]); for(k=0;k<G.vexnum;k++) printf("%d ",p[i][j][k]); printf("代价为:%d\n",D[i][j]); //printf("\n"); } } |
运行结果: